平差认为,或者说测量学的书籍认为,测量获得的值有一定的“误差”,需要进行“改正”,所以:真值=观测值+改正值 观测值=真值+误差
改正数和误差互为相反数。
在数学中,变量关系有两种基本类型:函数关系和相关关系(dependent relationship),此种关系没有密切到如上所述的确定关系。
假设因变量y和k个自变量x 1 , x 2 , ⋯ , x k x_1,x_2,\cdots,x_k x 1 , x 2 , ⋯ , x k y = β 0 + β 1 x 1 + ⋯ + β k x k + ε y=\beta_0+\beta_1x_1+\cdots+\beta_kx_k+\varepsilon y = β 0 + β 1 x 1 + ⋯ + β k x k + ε ε \varepsilon ε Y = X β + ε Y=X\beta+\varepsilon Y = X β + ε
其中Y = ( y 1 y 2 ⋮ y n ) , X = ( 1 x 1 1 … x 1 k 1 x 2 1 … x 2 k ⋮ ⋮ ⋮ 1 x n 1 … x n k ) , β = ( β 1 β 2 ⋮ β n ) , ε = ( ε 1 ε 2 ⋮ ε n ) , Y=
\begin{pmatrix}
y_1 \\ y_2 \\ \vdots \\y_n
\end{pmatrix},
X=\begin{pmatrix}
1 & x_{11} & \ldots & x_{1k}\\
1 & x_{21} & \ldots & x_{2k}\\
\vdots & \vdots & & \vdots \\
1 & x_{n1} & \ldots & x_{nk}
\end{pmatrix},
\beta=
\begin{pmatrix}
\beta_1 \\ \beta_2 \\ \vdots \\\beta_n
\end{pmatrix},
\varepsilon=
\begin{pmatrix}
\varepsilon_1 \\ \varepsilon_2 \\ \vdots \\\varepsilon_n
\end{pmatrix}, Y = ⎝ ⎜ ⎜ ⎛ y 1 y 2 ⋮ y n ⎠ ⎟ ⎟ ⎞ , X = ⎝ ⎜ ⎜ ⎛ 1 1 ⋮ 1 x 1 1 x 2 1 ⋮ x n 1 … … … x 1 k x 2 k ⋮ x n k ⎠ ⎟ ⎟ ⎞ , β = ⎝ ⎜ ⎜ ⎛ β 1 β 2 ⋮ β n ⎠ ⎟ ⎟ ⎞ , ε = ⎝ ⎜ ⎜ ⎛ ε 1 ε 2 ⋮ ε n ⎠ ⎟ ⎟ ⎞ , ε \varepsilon ε E ( ε ) = 0 , c o v ( ε , ε ) = Σ E(\varepsilon)=\mathbf 0,cov(\varepsilon,\varepsilon)=\Sigma E ( ε ) = 0 , c o v ( ε , ε ) = Σ 线性模型 ,记为( Y , X β , Σ ) (Y,X\beta,\Sigma) ( Y , X β , Σ ) 设计矩阵 (design matirx),β \beta β Σ \Sigma Σ Σ = σ 2 I n \Sigma=\sigma^2I_n Σ = σ 2 I n σ 2 \sigma^2 σ 2
Gauss-Markov条件:c o v ( ε , ε ) = σ 2 I n , E ( ε ) = 0 cov(\varepsilon,\varepsilon)=\sigma^2I_n,E(\varepsilon)=\mathbf{0} c o v ( ε , ε ) = σ 2 I n , E ( ε ) = 0
有时还需假定正态条件:ε ∼ N ( 0 , σ 2 I n ) \varepsilon\sim N(\mathbf{0},\sigma^2I_n) ε ∼ N ( 0 , σ 2 I n ) Y = X β + ε ∼ N ( X β , σ 2 I n ) Y=X\beta+\varepsilon\sim N(X\beta,\sigma^2I_n) Y = X β + ε ∼ N ( X β , σ 2 I n ) r a n k ( X ) = k + 1 rank(X)=k+1 r a n k ( X ) = k + 1
使偏离平方和∑ i = 1 n ( y i − y ~ i ) 2 \sum_{i=1}^n(y_i-\tilde y_i)^2 ∑ i = 1 n ( y i − y ~ i ) 2 β \beta β
y = β 0 + β 1 x + ε y=\beta_0+\beta_1x+\varepsilon y = β 0 + β 1 x + ε
假定E ( ε ) = 0 , v a r ( ε ) = σ 2 E(\varepsilon)=0,var(\varepsilon)=\sigma^2 E ( ε ) = 0 , v a r ( ε ) = σ 2
我们在这里讨论多元线性回归模型( Y , X β , σ 2 I n ) (Y,X\beta,\sigma^2I_n) ( Y , X β , σ 2 I n )
使总偏离平方和Q ( β ) = ∑ i = 1 n [ y i − ( β 0 + ∑ j = 1 k x i j β j ) ] 2 = ( Y − X β ) T ( Y − X β ) = ∣ ∣ Y − X β ∣ ∣ 2 \begin{aligned}
Q(\beta)&=\sum_{i=1}^n[y_i-(\beta_0+\sum_{j=1}^kx_{ij}\beta_j)]^2 \\
&= (Y-X\beta)^T(Y-X\beta)=||Y-X\beta||^2
\end{aligned} Q ( β ) = i = 1 ∑ n [ y i − ( β 0 + j = 1 ∑ k x i j β j ) ] 2 = ( Y − X β ) T ( Y − X β ) = ∣ ∣ Y − X β ∣ ∣ 2 β \beta β β ^ \hat\beta β ^ ∣ ∣ Y − X β ^ ∣ ∣ 2 = m i n β ∣ ∣ Y − X β ∣ ∣ 2 ||Y-X\hat\beta||^2=\underset{\beta}{min}||Y-X\beta||^2 ∣ ∣ Y − X β ^ ∣ ∣ 2 = β m i n ∣ ∣ Y − X β ∣ ∣ 2 β ^ \hat\beta β ^ β \beta β
Q = Q ( β ) = ( Y − X β ) T ( Y − X β ) = Y T Y − 2 β T X T Y + β T X T X β \begin{aligned}
Q=&Q(\beta)=(Y-X\beta)^T(Y-X\beta)\\
=& Y^TY-2\beta^TX^TY+\beta^TX^TX\beta
\end{aligned} Q = = Q ( β ) = ( Y − X β ) T ( Y − X β ) Y T Y − 2 β T X T Y + β T X T X β β \beta β ∂ Q ∂ β = − 2 X T Y + 2 X T X β = 0 \frac{\partial Q}{\partial \beta}=-2X^TY+2X^TX\beta=0 ∂ β ∂ Q = − 2 X T Y + 2 X T X β = 0 X T X β = X T Y X^TX\beta=X^TY X T X β = X T Y N = X T X N=X^TX N = X T X β ^ = ( X T X ) − 1 X T Y \hat\beta=(X^TX)^{-1}X^TY β ^ = ( X T X ) − 1 X T Y
因为存在偏导数为0的点不是极值点的情况,下面的定理告诉我们正规方程组的解就是β \beta β
定理 :
正规方程组的解(1)必是β \beta β
β \beta β
p r o o f . proof. p r o o f .
设β ~ \tilde\beta β ~ β ~ \tilde\beta β ~ ( X ′ X ) β ~ = X ′ Y (X'X)\tilde\beta=X'Y ( X ′ X ) β ~ = X ′ Y ∀ β , \forall \beta, ∀ β , Q ( β ) = ∣ ∣ Y − X β ∣ ∣ 2 = ( Y − X β ) ′ ( Y − X β ) = [ ( Y − X β ~ ) + X ( β ~ − β ) ] ′ [ ( Y − X β ~ ) + X ( β ~ − β ) ] = ( Y − X β ~ ) ′ ( Y − X β ~ ) + ( β ~ − β ) ′ X ′ X ( β ~ − β ) + 2 ( β − β ~ ) ′ X ′ ( Y − X β ~ ) \begin{aligned}
Q(\beta)=& ||Y-X\beta||^2=(Y-X\beta)'(Y-X\beta)\\
=& [(Y-X\tilde\beta)+X(\tilde\beta-\beta)]'[(Y-X\tilde\beta)+X(\tilde\beta-\beta)]\\
=& (Y-X\tilde\beta)' (Y-X\tilde\beta)+(\tilde\beta-\beta)'X'X(\tilde\beta-\beta)+2(\beta-\tilde\beta)'X'(Y-X\tilde\beta)
\end{aligned} Q ( β ) = = = ∣ ∣ Y − X β ∣ ∣ 2 = ( Y − X β ) ′ ( Y − X β ) [ ( Y − X β ~ ) + X ( β ~ − β ) ] ′ [ ( Y − X β ~ ) + X ( β ~ − β ) ] ( Y − X β ~ ) ′ ( Y − X β ~ ) + ( β ~ − β ) ′ X ′ X ( β ~ − β ) + 2 ( β − β ~ ) ′ X ′ ( Y − X β ~ ) ( β − β ~ ) ′ X ′ ( Y − X β ~ ) = ( β − β ~ ) ′ ( X ′ Y − X ′ X β ~ ) = 0 (\beta-\tilde\beta)'X'(Y-X\tilde\beta)=(\beta-\tilde\beta)'(X'Y-X'X\tilde\beta)=0 ( β − β ~ ) ′ X ′ ( Y − X β ~ ) = ( β − β ~ ) ′ ( X ′ Y − X ′ X β ~ ) = 0 ( β ~ − β ) ′ X ′ X ( β ~ − β ) = ∣ ∣ X ( β ~ − β ) ∣ ∣ 2 ≥ 0 (\tilde\beta-\beta)'X'X(\tilde\beta-\beta)=||X(\tilde\beta-\beta)||^2\ge 0 ( β ~ − β ) ′ X ′ X ( β ~ − β ) = ∣ ∣ X ( β ~ − β ) ∣ ∣ 2 ≥ 0 ∴ Q ( β ) ≥ ( Y − X β ~ ) ′ ( Y − X β ~ ) = Q ( β ~ ) \therefore Q(\beta)\ge (Y-X\tilde\beta)' (Y-X\tilde\beta)=Q(\tilde\beta) ∴ Q ( β ) ≥ ( Y − X β ~ ) ′ ( Y − X β ~ ) = Q ( β ~ ) ∣ ∣ X ( β ~ − β ) ∣ ∣ 2 = 0 ||X(\tilde\beta-\beta)||^2= 0 ∣ ∣ X ( β ~ − β ) ∣ ∣ 2 = 0 β \beta β β ~ \tilde\beta β ~ β ~ \tilde\beta β ~ β \beta β
设β ^ \hat\beta β ^ β \beta β β ~ \tilde\beta β ~ Q ( β ^ ) ≤ Q ( β ~ ) Q(\hat\beta)\le Q(\tilde\beta) Q ( β ^ ) ≤ Q ( β ~ ) Q ( β ~ ) ≤ Q ( β ^ ) Q(\tilde\beta)\le Q(\hat\beta) Q ( β ~ ) ≤ Q ( β ^ ) Q ( β ^ ) = Q ( β ~ ) Q(\hat\beta)=Q(\tilde\beta) Q ( β ^ ) = Q ( β ~ ) ( β ~ − β ) ′ X ′ X ( β ~ − β ) = ∣ ∣ X ( β ~ − β ) ∣ ∣ 2 = 0 (\tilde\beta-\beta)'X'X(\tilde\beta-\beta)=||X(\tilde\beta-\beta)||^2= 0 ( β ~ − β ) ′ X ′ X ( β ~ − β ) = ∣ ∣ X ( β ~ − β ) ∣ ∣ 2 = 0 X β ~ = X β ^ X\tilde\beta=X\hat\beta X β ~ = X β ^ β ~ \tilde\beta β ~ X ′ X β ^ = X ′ X β ~ = X ′ Y X'X\hat\beta=X'X\tilde\beta=X'Y X ′ X β ^ = X ′ X β ~ = X ′ Y β ^ \hat\beta β ^
设Y,Z为随机向量,A,B为常数矩阵,有下面两个常用结论:
E ( A Y ) = A E ( Y ) E(AY)=AE(Y) E ( A Y ) = A E ( Y ) c o v ( A Y , B Z ) = A c o v ( Y , Z ) B T cov(AY,BZ)=Acov(Y,Z)B^T c o v ( A Y , B Z ) = A c o v ( Y , Z ) B T
性质一 β ^ \hat\beta β ^ β \beta β p r o o f . proof. p r o o f . β ^ \hat\beta β ^ E ( β ^ ) = E ( ( X ′ X ) − 1 X ′ Y ) = ( X ′ X ) − 1 X ′ E ( Y ) = ( X ′ X ) − 1 X ′ X β = β E(\hat\beta)=E((X'X)^{-1}X'Y)=(X'X)^{-1}X'E(Y)=(X'X)^{-1}X'X\beta=\beta E ( β ^ ) = E ( ( X ′ X ) − 1 X ′ Y ) = ( X ′ X ) − 1 X ′ E ( Y ) = ( X ′ X ) − 1 X ′ X β = β
性质二 c o v ( β ^ , β ^ ) = σ 2 ( X ′ X ) − 1 = σ 2 N − 1 cov(\hat\beta,\hat\beta)=\sigma^2(X'X)^{-1}=\sigma^2N^{-1} c o v ( β ^ , β ^ ) = σ 2 ( X ′ X ) − 1 = σ 2 N − 1 p r o o f . proof. p r o o f . c o v ( β ^ , β ^ ) = c o v ( ( X ′ X ) − 1 X ′ Y , ( X ′ X ) − 1 X ′ Y ) = ( X ′ X ) − 1 X ′ c o v ( Y , Y ) X ( X ′ X ) − 1 = σ 2 ( X ′ X ) − 1 X ′ X ( X ′ X ) − 1 = σ 2 ( X ′ X ) − 1 \begin{aligned}
cov(\hat\beta,\hat\beta)&=cov((X'X)^{-1}X'Y,(X'X)^{-1}X'Y)\\
&=(X'X)^{-1}X'cov(Y,Y)X(X'X)^{-1}\\
&=\sigma^2(X'X)^{-1}X'X(X'X)^{-1}\\
&=\sigma^2(X'X)^{-1}
\end{aligned} c o v ( β ^ , β ^ ) = c o v ( ( X ′ X ) − 1 X ′ Y , ( X ′ X ) − 1 X ′ Y ) = ( X ′ X ) − 1 X ′ c o v ( Y , Y ) X ( X ′ X ) − 1 = σ 2 ( X ′ X ) − 1 X ′ X ( X ′ X ) − 1 = σ 2 ( X ′ X ) − 1 β ^ \hat\beta β ^
对任一k+1维向量C = ( c 0 , c 1 , … , c k ) ′ C=(c_0,c_1,\ldots,c_k)' C = ( c 0 , c 1 , … , c k ) ′ E ( L ′ Y ) = C ′ β E(L'Y)=C'\beta E ( L ′ Y ) = C ′ β C ′ β C'\beta C ′ β C ′ β C'\beta C ′ β 最好线性无偏估计 (Best Linear Unbiased Estimate,BLUE)
性质三 (Gauss-Markov定理):C ′ β ^ C'\hat\beta C ′ β ^ C ′ β C'\beta C ′ β β ^ \hat\beta β ^ β \beta β p r o o f . proof. p r o o f . C ′ β ^ C'\hat\beta C ′ β ^ C ′ β C'\beta C ′ β C ′ β C'\beta C ′ β T = L ′ Y T=L'Y T = L ′ Y v a r ( T ) ≥ v a r ( C ′ β ^ ) var(T)\ge var(C'\hat\beta) v a r ( T ) ≥ v a r ( C ′ β ^ ) T = L ′ Y T=L'Y T = L ′ Y C ′ β C'\beta C ′ β β \beta β E ( T ) = E ( L ′ Y ) = L ′ E ( Y ) = L ′ X β = C ′ β E(T)=E(L'Y)=L'E(Y)=L'X\beta=C'\beta E ( T ) = E ( L ′ Y ) = L ′ E ( Y ) = L ′ X β = C ′ β ∴ L ′ X = C ′ \therefore L'X=C' ∴ L ′ X = C ′ v a r ( T ) = v a r ( L ′ Y ) = L ′ c o v ( Y , Y ) L = σ 2 L ′ L var(T)=var(L'Y)=L'cov(Y,Y)L=\sigma^2L'L v a r ( T ) = v a r ( L ′ Y ) = L ′ c o v ( Y , Y ) L = σ 2 L ′ L v a r ( C ′ β ) = C ′ c o v ( β ^ , β ^ ) C = σ 2 C ( X ′ X ) − 1 C var(C'\beta)=C'cov(\hat\beta,\hat\beta)C=\sigma^2C(X'X)^{-1}C v a r ( C ′ β ) = C ′ c o v ( β ^ , β ^ ) C = σ 2 C ( X ′ X ) − 1 C 0 ≤ ∣ ∣ L − X ( X ′ X ) − 1 C ∣ ∣ 2 = L ′ L − C ′ ( X ′ X ) − 1 C ∴ v a r ( C ′ β ^ ) ≤ v a r ( T ) \begin{aligned}
0\le&||L-X(X'X)^{-1}C||^2\\
=&L'L-C'(X'X)^{-1}C\\
\therefore& var(C'\hat\beta)\le var(T)
\end{aligned} 0 ≤ = ∴ ∣ ∣ L − X ( X ′ X ) − 1 C ∣ ∣ 2 L ′ L − C ′ ( X ′ X ) − 1 C v a r ( C ′ β ^ ) ≤ v a r ( T ) C ′ β C'\beta C ′ β C ′ β ^ C'\hat\beta C ′ β ^ C ′ β C'\beta C ′ β
Gauss-Markov定理指出,C ′ β ^ C'\hat\beta C ′ β ^ C ′ β C'\beta C ′ β C ′ β C'\beta C ′ β C ′ β ^ C'\hat\beta C ′ β ^
性质四 在正态条件下,C ′ β ^ C'\hat\beta C ′ β ^ C ′ β C'\beta C ′ β
由最小二乘估计原理知道,在线性模型( Y , X β , σ 2 I n ) (Y,X\beta,\sigma^2I_n) ( Y , X β , σ 2 I n ) β \beta β β ^ \hat\beta β ^ Y ^ = X β ^ \hat Y=X\hat\beta Y ^ = X β ^ ε ^ = Y − Y ^ = Y − X β ^ \hat\varepsilon=Y-\hat Y=Y-X\hat\beta ε ^ = Y − Y ^ = Y − X β ^ 残差 ,关于残差有如下性质
性质五
E ( ε ^ ) = 0 E(\hat\varepsilon)=\mathbf{0} E ( ε ^ ) = 0 c o v ( ε ^ , ε ^ ) = σ 2 ( I n − X ( X ′ X ) − 1 X ′ ) cov(\hat\varepsilon,\hat\varepsilon)=\sigma^2(I_n-X(X'X)^{-1}X') c o v ( ε ^ , ε ^ ) = σ 2 ( I n − X ( X ′ X ) − 1 X ′ ) c o v ( β ^ , ε ^ ) = 0 cov(\hat\beta,\hat\varepsilon)=0 c o v ( β ^ , ε ^ ) = 0
1.式显然成立,下证另外两式。ε ^ = Y − X β ^ = Y − X ( X ′ X ) − 1 X ′ Y = ( I n − X ( X ′ X ) − 1 X ′ ) Y = △ A Y \begin{aligned}
\hat\varepsilon=&Y-X\hat\beta=Y-X(X'X)^{-1}X'Y\\
=&(I_n-X(X'X)^{-1}X')Y\overset{\triangle}{=}AY
\end{aligned} ε ^ = = Y − X β ^ = Y − X ( X ′ X ) − 1 X ′ Y ( I n − X ( X ′ X ) − 1 X ′ ) Y = △ A Y A = I n − X ( X ′ X ) − 1 X ′ A=I_n-X(X'X)^{-1}X' A = I n − X ( X ′ X ) − 1 X ′ A ′ = A , A 2 = A A'=A,A^2=A A ′ = A , A 2 = A c o v ( ε ^ , ε ^ ) = c o v ( A Y , A Y ) = A c o v ( Y , Y ) A ′ = σ 2 A A ′ = σ 2 A = σ 2 ( I n − X ( X ′ X ) − 1 X ′ ) c o v ( β ^ , ε ^ ) = c o v ( ( X ′ X ) − 1 X ′ Y , A Y ) = ( X ′ X ) − 1 X ′ c o v ( Y , Y ) A ′ = σ 2 ( X ′ X ) − 1 X ′ A = 0 \begin{aligned}
cov(\hat\varepsilon,\hat\varepsilon)=&cov(AY,AY)=Acov(Y,Y)A'\\
=&\sigma^2AA'=\sigma^2A=\sigma^2(I_n-X(X'X)^{-1}X')\\
cov(\hat\beta,\hat\varepsilon)=&cov((X'X)^{-1}X'Y,AY)\\
=&(X'X)^{-1}X'cov(Y,Y)A'\\
=&\sigma^2(X'X)^{-1}X'A=0
\end{aligned} c o v ( ε ^ , ε ^ ) = = c o v ( β ^ , ε ^ ) = = = c o v ( A Y , A Y ) = A c o v ( Y , Y ) A ′ σ 2 A A ′ = σ 2 A = σ 2 ( I n − X ( X ′ X ) − 1 X ′ ) c o v ( ( X ′ X ) − 1 X ′ Y , A Y ) ( X ′ X ) − 1 X ′ c o v ( Y , Y ) A ′ σ 2 ( X ′ X ) − 1 X ′ A = 0
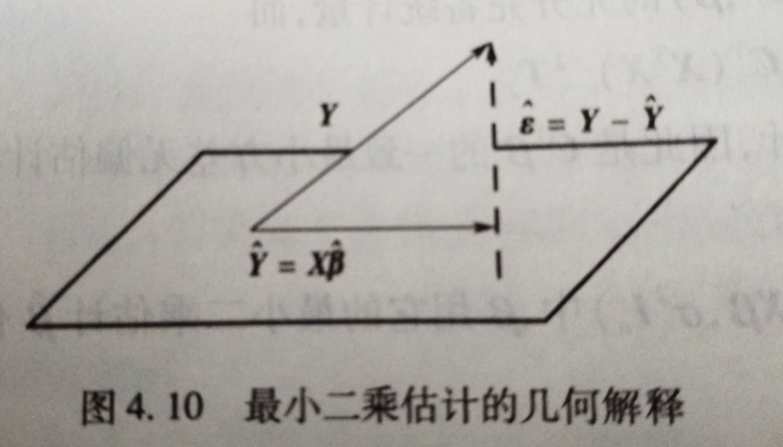
下面给出最小二乘估计几β ^ \hat\beta β ^ ε ^ \hat\varepsilon ε ^ ∣ ∣ Y ∣ ∣ = Y ′ Y ||Y||=\sqrt{Y'Y} ∣ ∣ Y ∣ ∣ = Y ′ Y
∣ ∣ Y 1 − Y 2 ∣ ∣ ||Y_1-Y_2|| ∣ ∣ Y 1 − Y 2 ∣ ∣
记设计矩阵的列向量为X 0 , X 1 , ⋯ , X k X_0,X_1,\cdots,X_k X 0 , X 1 , ⋯ , X k L ( X ) \mathscr L(X) L ( X ) β ^ , X β ^ ∈ L ( X ) \hat\beta,X\hat\beta\in\mathscr L(X) β ^ , X β ^ ∈ L ( X ) β ^ \hat\beta β ^ L ( X ) \mathscr L(X) L ( X ) X β ^ X\hat\beta X β ^ ε ^ \hat\varepsilon ε ^ X β ^ X\hat\beta X β ^ Y Y Y L ( X ) \mathscr L(X) L ( X ) X β ^ = X ( X ′ X ) − 1 X ′ Y X\hat\beta=X(X'X)^{-1}X'Y X β ^ = X ( X ′ X ) − 1 X ′ Y P = X ( X ′ X ) − 1 X ′ P=X(X'X)^{-1}X' P = X ( X ′ X ) − 1 X ′ L ( X ) \mathscr L(X) L ( X ) β ^ \hat\beta β ^ β \beta β ε ^ \hat\varepsilon ε ^ L ( X ) \mathscr L(X) L ( X ) Y ^ \hat Y Y ^ ε ^ \hat\varepsilon ε ^
记残差向量的长度平方,即Q e = ∣ ∣ ε ^ ∣ ∣ 2 = ε ^ ′ ε ^ Q_e=||\hat\varepsilon||^2=\hat\varepsilon'\hat\varepsilon Q e = ∣ ∣ ε ^ ∣ ∣ 2 = ε ^ ′ ε ^ Q e = ε ^ ′ ε ^ = ( Y − X β ^ ) ′ ( Y − X β ^ ) = ( A Y ) ′ ( A Y ) = Y ′ A Y = Y ′ Y − Y ′ X ( X ′ X ) − 1 ( X ′ X ) ( X ′ X ) − 1 X ′ Y = Y ′ Y − β ^ ′ X ′ X β ^ = Y ′ Y − Y ^ ′ X β ^ = Y ′ Y − Y ^ ′ Y ^ \begin{aligned}
Q_e=&\hat\varepsilon'\hat\varepsilon=(Y-X\hat\beta)'(Y-X\hat\beta)=(AY)'(AY)\\
=&Y'AY=Y'Y-Y'X(X'X)^{-1}(X'X)(X'X)^{-1}X'Y\\
=&Y'Y-\hat\beta'X'X\hat\beta=Y'Y-\hat Y'X\hat\beta\\
=& Y'Y-\hat Y'\hat Y
\end{aligned} Q e = = = = ε ^ ′ ε ^ = ( Y − X β ^ ) ′ ( Y − X β ^ ) = ( A Y ) ′ ( A Y ) Y ′ A Y = Y ′ Y − Y ′ X ( X ′ X ) − 1 ( X ′ X ) ( X ′ X ) − 1 X ′ Y Y ′ Y − β ^ ′ X ′ X β ^ = Y ′ Y − Y ^ ′ X β ^ Y ′ Y − Y ^ ′ Y ^ ε ^ \hat\varepsilon ε ^ Y ^ \hat Y Y ^ Y Y Y Q e Q_e Q e
残差ε ^ \hat\varepsilon ε ^ σ 2 \sigma^2 σ 2 Q e = ∣ ∣ ε ^ ∣ ∣ 2 Q_e=||\hat\varepsilon||^2 Q e = ∣ ∣ ε ^ ∣ ∣ 2 σ 2 \sigma^2 σ 2
证明残差的平方和与σ 2 \sigma^2 σ 2
设n维随机向量Y,有E ( Y ) = a , c o v ( Y , Y ) = σ 2 I n , A E(Y)=a,cov(Y,Y)=\sigma^2I_n,A E ( Y ) = a , c o v ( Y , Y ) = σ 2 I n , A E ( Y ′ A Y ) = a ′ A a + σ 2 t r ( A ) E(Y'AY)=a'Aa+\sigma^2tr(A) E ( Y ′ A Y ) = a ′ A a + σ 2 t r ( A )
设A,B是两个使乘积AB,BA都为方阵的矩阵,则t r ( A B ) = t r ( B A ) tr(AB)=tr(BA) t r ( A B ) = t r ( B A )
t r ( A + B ) = t r ( A ) + t r ( B ) tr(A+B)=tr(A)+tr(B) t r ( A + B ) = t r ( A ) + t r ( B )
性质六 记σ ^ 2 = Q e n − ( k + 1 ) = Q e n − t \hat\sigma^2=\frac{Q_e}{n-(k+1)}=\frac{Q_e}{n-t} σ ^ 2 = n − ( k + 1 ) Q e = n − t Q e E ( σ ^ 2 ) = σ 2 E(\hat\sigma^2)=\sigma^2 E ( σ ^ 2 ) = σ 2 p r o o f . proof. p r o o f . E ( Q e ) = E ( Y ′ A Y ) = β ′ X ′ [ I n − X ( X ′ X ) − 1 X ′ ] X β + σ 2 t r [ I n − X ′ ( X ′ X ) − 1 X ′ ] = σ 2 t r ( I n − X ( X ′ X ) − 1 X ′ ) = σ 2 [ n − t r [ X ( X ′ X ) − 1 X ′ ] ] = σ 2 [ n − t r ( I k + 1 ) ] = σ 2 ( n − k − 1 ) \begin{aligned}
E(Q_e)=& E(Y'AY)\\
=& \beta'X'[I_n-X(X'X)^{-1}X']X\beta+\sigma^2tr[I_n-X'(X'X)^{-1}X']\\
=& \sigma^2tr(I_n-X(X'X)^{-1}X')\\
=& \sigma^2[n-tr[X(X'X)^{-1}X']]\\
=& \sigma^2[n-tr(I_{k+1})]\\
=& \sigma^2(n-k-1)
\end{aligned} E ( Q e ) = = = = = = E ( Y ′ A Y ) β ′ X ′ [ I n − X ( X ′ X ) − 1 X ′ ] X β + σ 2 t r [ I n − X ′ ( X ′ X ) − 1 X ′ ] σ 2 t r ( I n − X ( X ′ X ) − 1 X ′ ) σ 2 [ n − t r [ X ( X ′ X ) − 1 X ′ ] ] σ 2 [ n − t r ( I k + 1 ) ] σ 2 ( n − k − 1 ) E ( σ ^ 2 ) = E ( Q e n − k − 1 ) = σ 2 E(\hat\sigma^2)=E(\frac{Q_e}{n-k-1})=\sigma^2 E ( σ ^ 2 ) = E ( n − k − 1 Q e ) = σ 2
性质七 在正态性条件下
β ^ , ε ^ \hat\beta,\hat\varepsilon β ^ , ε ^ β ^ ∼ N ( β , σ 2 N − 1 ) , ε ^ ∼ N ( 0 , σ 2 A ) \hat\beta\sim N(\beta,\sigma^2N^{-1}),\hat\varepsilon\sim N(\mathbf 0,\sigma^2 A) β ^ ∼ N ( β , σ 2 N − 1 ) , ε ^ ∼ N ( 0 , σ 2 A ) β ^ , Q e \hat\beta,Q_e β ^ , Q e Q e σ 2 ∼ χ 2 ( n − k − 1 ) \frac{Q_e}{\sigma^2}\sim\chi^2(n-k-1) σ 2 Q e ∼ χ 2 ( n − k − 1 )
由性质一,二,五知1.2.显然成立下证3.p r o o f . proof. p r o o f . Q e = Y ′ A Y = ( X β + ε ) ′ A ( X β + ε ) = β ′ X ′ A X β + β ′ X ′ A ε + ε ′ A X β + ε ′ A ε \begin{aligned}
Q_e=&Y'AY=(X\beta+\varepsilon)'A(X\beta+\varepsilon)\\
=& \beta'X'AX\beta+\beta'X'A\varepsilon+\varepsilon'AX\beta+\varepsilon'A\varepsilon
\end{aligned} Q e = = Y ′ A Y = ( X β + ε ) ′ A ( X β + ε ) β ′ X ′ A X β + β ′ X ′ A ε + ε ′ A X β + ε ′ A ε A = I n − X ( X ′ X ) − 1 X ′ A=I_n-X(X'X)^{-1}X' A = I n − X ( X ′ X ) − 1 X ′ β ′ X ′ A X β = 0 \beta'X'AX\beta=0 β ′ X ′ A X β = 0 β ′ X ′ A = A X β = 0 \beta'X'A=AX\beta=0 β ′ X ′ A = A X β = 0 Q e = ε ′ A ε Q_e=\varepsilon'A\varepsilon Q e = ε ′ A ε ε \varepsilon ε Γ \Gamma Γ A = Γ T Λ Γ , A=\Gamma^T\Lambda\Gamma, A = Γ T Λ Γ , Λ = d i a g ( λ 1 , ⋯ , λ n ) , λ 1 , ⋯ , λ n \Lambda=diag(\lambda_1,\cdots,\lambda_n),\lambda_1,\cdots,\lambda_n Λ = d i a g ( λ 1 , ⋯ , λ n ) , λ 1 , ⋯ , λ n λ i \lambda_i λ i r a n k ( A ) = t r ( A ) = n − k − 1 , rank(A)=tr(A)=n-k-1, r a n k ( A ) = t r ( A ) = n − k − 1 , λ 1 = ⋯ = λ n − k − 1 = 1 \lambda_1=\cdots=\lambda_{n-k-1}=1 λ 1 = ⋯ = λ n − k − 1 = 1 e = Γ ε / σ e=\Gamma\varepsilon/\sigma e = Γ ε / σ ε ∼ N ( 0 , σ 2 I n ) \varepsilon\sim N(0,\sigma^2I_n) ε ∼ N ( 0 , σ 2 I n ) Γ \Gamma Γ e ∼ N ( 0 , I n ) e\sim N(0,I_n) e ∼ N ( 0 , I n ) e = ( e 1 , ⋯ , e n ) ′ e=(e_1,\cdots,e_n)' e = ( e 1 , ⋯ , e n ) ′ e i e_i e i N ∼ ( 0 , 1 ) N\sim(0,1) N ∼ ( 0 , 1 ) Q e σ 2 = ( ε σ ) ′ Γ ′ Γ A Γ ′ Γ ( ε σ ) = e ′ Λ e = ∑ i = 1 n − k − 1 e i 2 ∼ χ 2 ( n − k − 1 ) \frac{Q_e}{\sigma^2}=(\frac{\varepsilon}{\sigma})'\Gamma'\Gamma A\Gamma'\Gamma(\frac{\varepsilon}{\sigma})=e'\Lambda e=\sum_{i=1}^{n-k-1}e_i^2\sim\chi^2(n-k-1) σ 2 Q e = ( σ ε ) ′ Γ ′ Γ A Γ ′ Γ ( σ ε ) = e ′ Λ e = i = 1 ∑ n − k − 1 e i 2 ∼ χ 2 ( n − k − 1 )
性质八 若ε ∼ N ( 0 , σ 2 I n ) \varepsilon\sim N(0,\sigma^2I_n) ε ∼ N ( 0 , σ 2 I n ) β \beta β β ^ \hat\beta β ^ β \beta β σ 2 \sigma^2 σ 2 Q e / n Q_e/n Q e / n p r o o f . proof. p r o o f . ε ∼ N ( 0 , σ 2 I n ) , Y ∼ N ( X β , σ 2 I n ) \varepsilon\sim N(0,\sigma^2I_n),Y\sim N(X\beta,\sigma^2I_n) ε ∼ N ( 0 , σ 2 I n ) , Y ∼ N ( X β , σ 2 I n ) f ( Y ; β , σ 2 ) = ( 2 π σ 2 ) − n / 2 exp [ − 1 2 σ 2 ( Y − X β ) ′ ( Y − X β ) ] f(Y;\beta,\sigma^2)=(2\pi\sigma^2)^{-n/2}\exp[-\frac{1}{2\sigma^2}(Y-X\beta)'(Y-X\beta)] f ( Y ; β , σ 2 ) = ( 2 π σ 2 ) − n / 2 exp [ − 2 σ 2 1 ( Y − X β ) ′ ( Y − X β ) ] ln L ( β , σ 2 ) = − n 2 ln 2 π − n 2 ln σ 2 − 1 2 σ 2 ( Y − X β ) ′ ( Y − X β ) \ln L(\beta,\sigma^2)=-\frac{n}{2}\ln 2\pi-\frac{n}{2}\ln\sigma^2-\frac{1}{2\sigma^2}(Y-X\beta)'(Y-X\beta) ln L ( β , σ 2 ) = − 2 n ln 2 π − 2 n ln σ 2 − 2 σ 2 1 ( Y − X β ) ′ ( Y − X β ) { ∂ ln L ∂ β = − 1 2 σ 2 ( − 2 X ′ Y + 2 X ′ X β ) ∂ ln L ∂ σ 2 = − n 2 σ 2 + 1 2 σ 4 ( Y − X β ) ′ ( Y − X β ) \begin{cases}
\frac{\partial \ln L}{\partial \beta}=-\frac{1}{2\sigma^2}(-2X'Y+2X'X\beta)\\
\frac{\partial \ln L}{\partial\sigma^2}=-\frac{n}{2\sigma^2}+\frac{1}{2\sigma^4}(Y-X\beta)'(Y-X\beta)
\end{cases} { ∂ β ∂ ln L = − 2 σ 2 1 ( − 2 X ′ Y + 2 X ′ X β ) ∂ σ 2 ∂ ln L = − 2 σ 2 n + 2 σ 4 1 ( Y − X β ) ′ ( Y − X β ) β ^ L = ( X ′ X ) − 1 X ′ Y \hat\beta_L=(X'X)^{-1}X'Y β ^ L = ( X ′ X ) − 1 X ′ Y σ ^ L 2 = 1 n ( Y − X β ^ L ) ′ ( Y − X β ^ L ) = Q e n \hat\sigma^2_L=\frac{1}{n}(Y-X\hat\beta_L)'(Y-X\hat\beta_L)=\frac{Q_e}{n} σ ^ L 2 = n 1 ( Y − X β ^ L ) ′ ( Y − X β ^ L ) = n Q e
在线性回归模型( Y , X β , σ 2 I n ) (Y,X\beta,\sigma^2I_n) ( Y , X β , σ 2 I n ) c o v ( Y , Y ) = σ 2 I n cov(Y,Y)=\sigma^2I_n c o v ( Y , Y ) = σ 2 I n c o v ( Y , Y ) = σ 2 Q cov(Y,Y)=\sigma^2 Q c o v ( Y , Y ) = σ 2 Q ∣ Q ∣ ≠ 0 |Q|\neq 0 ∣ Q ∣ ≠ 0 ( Y , X β , σ 2 Q ) (Y,X\beta,\sigma^2Q) ( Y , X β , σ 2 Q )
定义:设A是一个n阶复矩阵,如果存在一个n阶复矩阵B使A = B 2 A=B^2 A = B 2 B = A B=\sqrt A B = A
为了求未知参数β , σ 2 \beta,\sigma^2 β , σ 2 Z = Q − 1 / 2 Y , U = Q − 1 / 2 X Z=Q^{-1/2}Y,U=Q^{-1/2}X Z = Q − 1 / 2 Y , U = Q − 1 / 2 X E ( Z ) = E ( Q − 1 / 2 Y ) = Q − 1 / 2 E ( Y ) = Q − 1 / 2 X β = U β E(Z)=E(Q^{-1/2}Y)=Q^{-1/2}E(Y)=Q^{-1/2}X\beta=U\beta E ( Z ) = E ( Q − 1 / 2 Y ) = Q − 1 / 2 E ( Y ) = Q − 1 / 2 X β = U β c o v ( Z , Z ) = c o v ( Q − 1 / 2 Y , Q − 1 / 2 Y ) = σ 2 Q − 1 / 2 ⋅ Q ⋅ Q − 1 / 2 = σ 2 I n cov(Z,Z)=cov(Q^{-1/2}Y,Q^{-1/2}Y)=\sigma^2Q^{-1/2}\cdot Q\cdot Q^{-1/2}=\sigma^2I_n c o v ( Z , Z ) = c o v ( Q − 1 / 2 Y , Q − 1 / 2 Y ) = σ 2 Q − 1 / 2 ⋅ Q ⋅ Q − 1 / 2 = σ 2 I n ( Y , X β , σ 2 Q ) (Y,X\beta,\sigma^2 Q) ( Y , X β , σ 2 Q ) ( Z , U β , σ 2 I n ) (Z,U\beta,\sigma^2I_n) ( Z , U β , σ 2 I n ) U ′ U β = U ′ Z U'U\beta=U'Z U ′ U β = U ′ Z X ′ Q − 1 X β = X ′ Q − 1 Y X'Q^{-1}X\beta=X'Q^{-1}Y X ′ Q − 1 X β = X ′ Q − 1 Y P = Q − 1 P=Q^{-1} P = Q − 1 β ^ = ( X ′ P X ) − 1 X ′ P Y \hat\beta=(X'PX)^{-1}X'PY β ^ = ( X ′ P X ) − 1 X ′ P Y β \beta β c o v ( β ^ , β ^ ) = σ 2 ( U ′ U ) − 1 = σ 2 ( X ′ P X ) − 1 cov(\hat\beta,\hat\beta)=\sigma^2(U'U)^{-1}=\sigma^2(X'PX)^{-1} c o v ( β ^ , β ^ ) = σ 2 ( U ′ U ) − 1 = σ 2 ( X ′ P X ) − 1 Q e = ∣ ∣ Z − U β ^ ∣ ∣ 2 = ∣ ∣ Q − 1 / 2 Y − Q − 1 / 2 X ( X ′ P X ) − 1 X ′ P Y ∣ ∣ 2 = Y ′ P Y − Y ′ P X ( X ′ P X ) − 1 X ′ P Y = Y ′ P Y − Y ′ P X β ^ \begin{aligned}
Q_e=||Z-U\hat\beta||^2=&||Q^{-1/2}Y-Q^{-1/2}X(X'PX)^{-1}X'PY||^2\\
=& Y'PY-Y'PX(X'PX)^{-1}X'PY\\
=& Y'PY-Y'PX\hat\beta
\end{aligned} Q e = ∣ ∣ Z − U β ^ ∣ ∣ 2 = = = ∣ ∣ Q − 1 / 2 Y − Q − 1 / 2 X ( X ′ P X ) − 1 X ′ P Y ∣ ∣ 2 Y ′ P Y − Y ′ P X ( X ′ P X ) − 1 X ′ P Y Y ′ P Y − Y ′ P X β ^
记:S y y = ∑ ( y i − y ¯ ) 2 = ∣ ∣ Y − 1 y ¯ ∣ ∣ 2 S_{yy}=\sum(y_i-\bar y)^2=||Y-\mathbf 1\bar y||^2 S y y = ∑ ( y i − y ¯ ) 2 = ∣ ∣ Y − 1 y ¯ ∣ ∣ 2 Q e = ∣ ∣ Y − Y ^ ∣ ∣ 2 Q_e=||Y-\hat Y||^2 Q e = ∣ ∣ Y − Y ^ ∣ ∣ 2 U = ∣ ∣ Y ^ − 1 y ¯ ∣ ∣ 2 = ∑ ( y ^ i − y ¯ ) 2 U=||\hat Y-\mathbf 1\bar y||^2=\sum (\hat y_i-\bar y)^2 U = ∣ ∣ Y ^ − 1 y ¯ ∣ ∣ 2 = ∑ ( y ^ i − y ¯ ) 2 y ^ i \hat y_i y ^ i S y y = Q e + U S_{yy}=Q_e+U S y y = Q e + U S y y = ∣ ∣ Y − 1 y ¯ ∣ ∣ 2 = ∣ ∣ ( Y − Y ^ ) + ( Y ^ − 1 y ¯ ) ∣ ∣ 2 = ∣ ∣ Y − Y ^ ∣ ∣ 2 + ∣ ∣ Y ^ − 1 y ¯ ∣ ∣ 2 + 2 ( Y − Y ^ ) ′ ( Y ^ − 1 y ¯ ) \begin{aligned}
S_{yy}=& ||Y-1\bar y||^2=||(Y-\hat Y)+(\hat Y-1\bar y)||^2\\
=&||Y-\hat Y||^2+||\hat Y-1\bar y||^2+2(Y-\hat Y)'(\hat Y-1\bar y)
\end{aligned} S y y = = ∣ ∣ Y − 1 y ¯ ∣ ∣ 2 = ∣ ∣ ( Y − Y ^ ) + ( Y ^ − 1 y ¯ ) ∣ ∣ 2 ∣ ∣ Y − Y ^ ∣ ∣ 2 + ∣ ∣ Y ^ − 1 y ¯ ∣ ∣ 2 + 2 ( Y − Y ^ ) ′ ( Y ^ − 1 y ¯ ) A P = 0 AP=0 A P = 0 ( Y − Y ^ ) ′ 1 = 0 (Y-\hat Y)'\mathbf{1}=0 ( Y − Y ^ ) ′ 1 = 0 ( Y − Y ^ ) ′ ( Y ^ − 1 y ¯ ) = ( Y − Y ^ ) ′ Y ^ − ( Y − Y ^ ) ′ 1 y ¯ = { [ I n − X ( X ′ X ) − 1 X ′ ] Y } ′ [ X ( X ′ X ) − 1 X ′ Y ] = Y ′ A P Y = 0 \begin{aligned}
(Y-\hat Y)'(\hat Y-1\bar y)=&(Y-\hat Y)'\hat Y-(Y-\hat Y)'1\bar y\\
=& \{[I_n-X(X'X)^{-1}X']Y \}'[X(X'X)^{-1}X'Y]\\
=& Y'APY=0
\end{aligned} ( Y − Y ^ ) ′ ( Y ^ − 1 y ¯ ) = = = ( Y − Y ^ ) ′ Y ^ − ( Y − Y ^ ) ′ 1 y ¯ { [ I n − X ( X ′ X ) − 1 X ′ ] Y } ′ [ X ( X ′ X ) − 1 X ′ Y ] Y ′ A P Y = 0
应用数理统计(第二版) 关静,张玉环,史道济 主编