平差与统计的区别

平差和统计的概念区别

平差认为，或者说测量学的书籍认为，测量获得的值有一定的“误差”，需要进行“改正”，所以：
真值=观测值+改正值
而统计中和物理学中认为观测值是真值加上一些误差（或者称“噪声”）引起的，所以：
观测值=真值+误差
在摄影测量和数据处理的相关教材中沿用此规定。本文以统计的概念入手，所以沿用此规定，希望读者注意区别。

改正数和误差互为相反数。

认识线性回归

• 函数关系:$Y=f(X)$
• 相关关系:$Y=f(X)+\varepsilon$
• 相关关系最直接的描述：散点图
• 如果X，Y两个随机变量的分布已知，总体的线性相关系数：$\rho=\frac{cov(X,Y)}{\sqrt{var(X)var(Y)}}$
• 实际上从统计的角度来讲，总体永远是未知的，即的样本的线性相关系数：$\gamma_{XY}=\frac{\sum(X_i-\bar X)(Y_i-\bar Y)}{\sqrt{\sum(X_i-\bar X)^2\sum (Y_i-\bar Y)^2}}$
• 样本相关系数是总体相关系数的估计，由于抽样波动，样本相关系数是随机变量，其显著性有待检验。
• 回归的现代意义：一个应变量对若干解释变量依存关系的研究
• 回归的目的：由固定的解释变量去估计应变量的平均值。
  
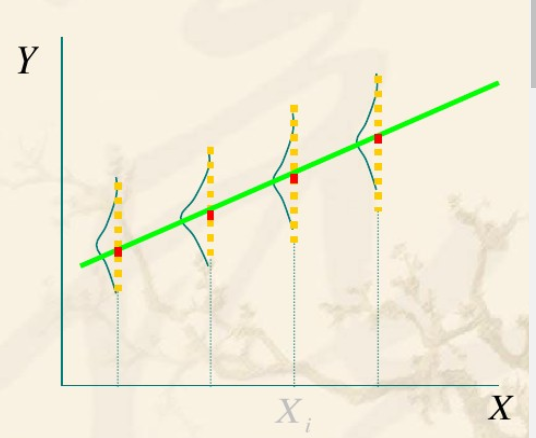
• Y的条件分布：当解释变量X取定(条件)，Y的值不确定，由Y的不同取值形成一定的分布，即Y的条件分布
• Y的条件期望：对于X的每一个取值，对Y所形成的分布的期望，称为Y的条件期望$E(Y|X_i)$
• 回归线：对于每一个X的取值，都有Y的条件期望$E(Y|X_i)$与之对应，代表这些Y的条件期望的点的轨迹的直线或曲线，称为回归线。
• 回归函数：因变量Y的条件期望$E(Y|X_i)$随解释变量X的变化而有规律的变化，将Y的条件期望表现为X的某种函数
  $E(Y|X_i)=f(X_i)$
  这个函数称为回归函数。
  回归函数分为：总体回归函数（PRF,总体已知）和样本回归函数（SRF，总体未知）。
• 总体回归函数的表现形式
  • 条件均值的表现形式$E(Y|X_i)=f(X_i)=\beta_0+\beta_1X_i$
  • 个别值的表现形式：取定$X_i$,Y的各个别值$Y_i$（样本）分布在条件均值$E(Y|X_i)$周围，定义随机变量$u_i$
    $u_i=Y_i-E(Y_i|X_i)$即$Y_i=E(Y_i|X_i)+u_i$
  • 线性回归模型的“线性”有两种解释：
    • 对变量而言是线性的：Y的条件均值是X的线性函数
    • 对参数而言是线性的：Y的条件均值是参数$\beta$的线性函数
      线性回归模型主要指对参数而言是“线性”的
• 样本回归函数SRF
  • 对于总体中的一个样本$X=(X_1,\cdots,X_n),Y=(Y_1,\cdots,Y_n)$,画一条直线拟合该散点图，这条直线称为样本回归线。
  • 记样本回归函数为：
    $\hat Y_i=f(X_i)=\hat\beta_0+\hat\beta_iX_i$
  • 将样本回归线看做总体回归线的近似。
    • $\hat Y_i=f(X_i)=\hat\beta_0+\hat\beta_iX_i$与$Y_i=E(Y|X_i)+u_i$,则$\hat Y_i$为$E(Y|X_i)$的估计量
    • $\hat\beta_i$为$\beta_i$的估计量。
  • 样本回归函数的随机形式/样本回归模型
    $Y_i=\hat Y_i+\hat u_i=\hat\beta_0+\hat\beta_1X_i+e_i$式中，$e_i$称为残差(residual)。代表了其他影响$Y_i$的随机因素的集合，可以看成$u_i$的估计量$\hat u_i$
  • 关系示意图：
    
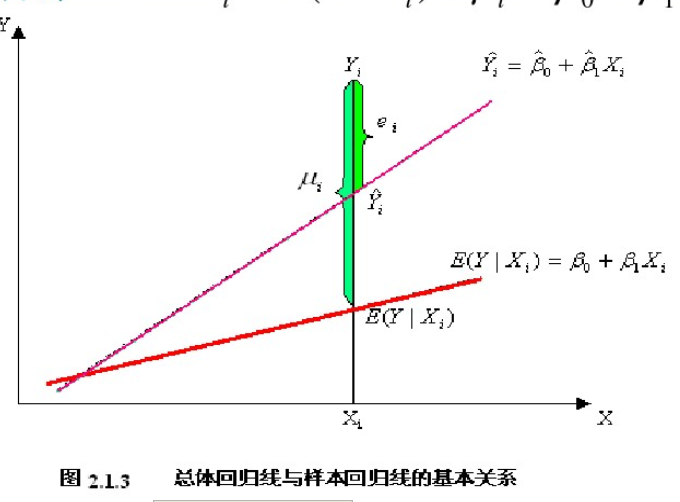
• 线性回归的模型的基本假设：
  • 假设一：解释变量X是确定性变量，不是随机变量
  • 假设二：随机误差项u具有零均值，同方差和无自相关。
  • 假设三：随机误差u与解释变量X不相关
  • 假设四：u服从零均值，同方差，零协方差的正态分布
    $u\sim N(\mathbf 0,\sigma^2 I_n)$
    注意：如果假设1，2满足，则假设3满足。如果假设4满足，则假设2也满足
    以上假设称为线性回归模型的经典假设或高斯假设，满足该假设的线性回归模型称为经典线性回归模型(Classical Linear Regression Model,CLRM)

认识随机变量

在线性回归模型$(Y,X\beta,\sigma^2I_n)$中：
$Y=X\beta+\varepsilon$

由于我们是站在观测之前的立场上，认为$Y,\varepsilon$是两个个随机向量（参数$\beta$不具有随机性，参数的估计$\hat\beta$才具有随机性），$X$是已知的。其中参数$\beta,\sigma$为待估参数，当Y值观测之后，$\varepsilon$的值也就只是$\beta$的函数，就可以对其求极值，进行最小二乘估计。

区别

在间接平差（参数平差）中，一般将线性模型叫高斯—马尔柯夫模型（G-M模型），记为$\tilde L=L+\Delta=B\tilde X,D(L)=D(\Delta)=\sigma_0^2Q$,称Q为协因数阵（权逆阵）。

参考资料

1. 经典线性回归模型https://wenku.baidu.com/view/a24e1bbd9e3143323968938f.html