坐标系的旋转与欧拉角

Definition

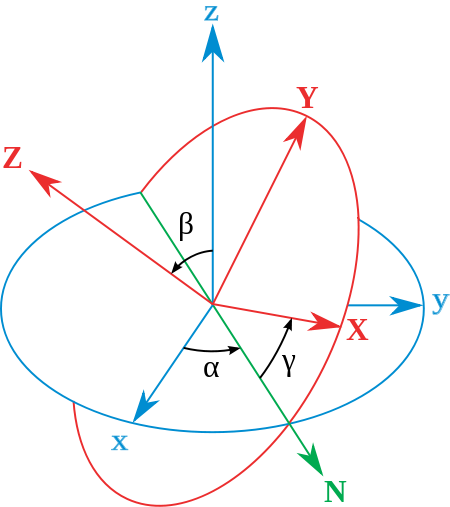
先绕z轴旋转α角，再绕x'旋转β角，最后绕z''旋转γ角，这组欧拉角被称为"zxz顺规"，以下结论均采用此顺序。
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body with respect to a fixed coordinate system.[1] They can also represent the orientation of a mobile frame of reference in physics or the orientation of a general basis in 3-dimensional linear algebra.

三维空间的刚体绕定点旋转。

Euler angles are typically denoted as $\alpha,\beta,\gamma,or\ \varphi,\theta,\psi$

Tait–Bryan angles are also called Cardan angles; nautical angles; heading, elevation, and bank; or yaw(偏航角), pitch(俯仰角), and roll(横滚角). Sometimes, both kinds of sequences are called "Euler angles". In that case, the sequences of the first group are called proper or classic Euler angles.

Geometrical definition

The axes of the original frame are denoted as x,y,z and the axes of the rotated frame as X,Y,Z. The geometrical definition (sometimes referred to as static) begins by defining the line of nodes as the intersection of the planes xy and XY (it can also be defined as the common perpendicular(公垂线) to the axes z and Z and then written as the vector product $N = z\times Z$). Using it, the three Euler angles can be defined as follows:

• $\alpha\ or\ \varphi$ is the angle between the x axis and the N axis (x-convention - it could also be defined between y and N, called y-convention).
• $\beta\ or\ \theta$ is the angle between the z axis and the Z axis.
• $\gamma\ or\ \psi$ is the angle between the N axis and the X axis (x-convention).
  Euler angles between two reference frames are defined only if both frames have the same handedness(手性).

Definition by intrinsic(本质的) rotation

Intrinsic rotations are elemental rotations that occur about the axes of a coordinate system XYZ attached to a moving body. Therefore, they change their orientation after each elemental rotation. The XYZ system rotates, while xyz is fixed. Starting with XYZ overlapping xyz, a composition of three intrinsic rotations can be used to reach any target orientation for XYZ.

• x-y-z, or x0-y0-z0 (initial)
• x’-y’-z’, or x1-y1-z1 (after first rotation)
• x″-y″-z″, or x2-y2-z2 (after second rotation)
• X-Y-Z, or x3-y3-z3 (final)

Signs and ranges

• for α and γ, the range is defined modulo 2π radians. For instance, a valid range could be [−π, π).
• for β, the range covers π radians (but can't be said to be modulo π). For example, it could be [0, π] or [−π/2, π/2].

矩阵表示

定义三个旋转矩阵
$R_x(\theta)= \begin{pmatrix} 1 & 0 & 0\\ 0 & \cos \theta & -\sin\theta \\ 0 & \sin \theta & \cos\theta \end{pmatrix}$
$R_y(\theta)= \begin{pmatrix} \cos \theta & 0 & -\sin\theta\\ 0 & 1 & 0\\ \sin \theta & 0 & \cos\theta \end{pmatrix}$
$R_z(\theta)= \begin{pmatrix} \cos \theta & -\sin\theta &0 \\ \sin \theta & \cos\theta &0\\ 0 & 0 & 1 \end{pmatrix}$

点变换

分别表示绕$x,y,z$轴旋转$\theta$角
旋转之前在$O-xyz$的坐标$a=(x,y,z)^T$
旋转之后在$O-xyz$的坐标$a'=(x',y',z')^T$,有
$a'=R_z(\alpha)R_x(\beta)R_z(\gamma)a$

坐标变换

基变换：$e'=eR_z(\alpha)R_x(\beta)R_z(\gamma)$,故

设一点在旧坐标系的坐标为a,在新坐标系的坐标为A，则
$a=R_z(\alpha)R_x(\beta)R_z(\gamma)A$

手机坐标系

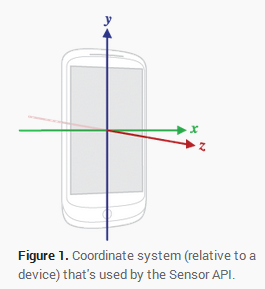
第一个角度：Azimuth 方位角
手机的偏航角定义为方位角A(Azimuth)$\in[0,2\pi)$,从y轴顺时针旋转的角度。
第二个角度：Pitch 俯仰角(degrees of rotation around x axis)
机头向下为正，向上为负。
第三个角度：Roll 横滚角(degrees of rotation around y axis)
绕y轴逆时针为正，顺时针为负。

References

1. Euler angles, wikipedia