此文目的:用射影几何用语来解释摄影测量词汇。
记号:前面的记号为摄影测量中的记号,后面的记号为射影几何中的记号。摄影测量中的记号以大写字母表示地平面上的点,以小写字母表示像平面上的点。
本文需要一定的射影几何基础。
参见:
射影几何(一)
射影几何(二)

设像平面P为π1,地平面E为π0。摄影物镜后节点S为投影中心O。此中心射影为π0→π1以O为投影中心的中心射影。以下将与地平面平行的平面称为水平面,与地平面垂直的平面称为竖直面。
- 透视轴、迹线TT:自对应直线π0×π1
- 像主点o:像平面的正截影P'
- 主距f/So:像主点到投影中心O的距离OP'
- 地主点O:像主点的原象
- 摄影方向:OP⃗的方向
- 地底点N:地平面的正截影
- 像底点n:地底点的象
- 航高SN:地底点到投影中心O的距离
- 主垂面W:过O点与π0与π1都垂直的平面(公垂面)
- 主纵线vv:主垂面在像平面上的截影
- 摄影方向线VV:主垂面在地平面上的截影
- 倾角α:π0与π1的所成的二面角
- 等角点(C,c):地主点与地底点的射影的角平分线的截影
- 合点(灭点):像平面上的影消点
- 合线hihi(真水平线):像平面上的影消线
- 合面(真水平面)Es:像平面上影消线的射影
- 主合点i:像平面上的影消线与主垂面的交点N。
- 像水平线:像平面上影消线的平行线
- 等比线hchc:过等角点c的像水平线
- 主遁点J:地平面上影消线与主垂面的交点M
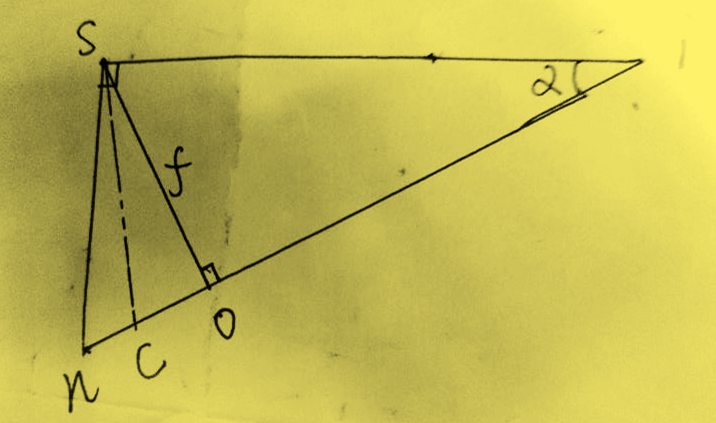
易知,△iSo为等腰三角形。
长度关系
on=oc=oi=ci=ftanαftan2αfcotαsinαf
三角关系式
tan2α+cotα=sinα1
proof.
设tan2α=t
由万能公式
left==t+2t1−t22t1+t2=right
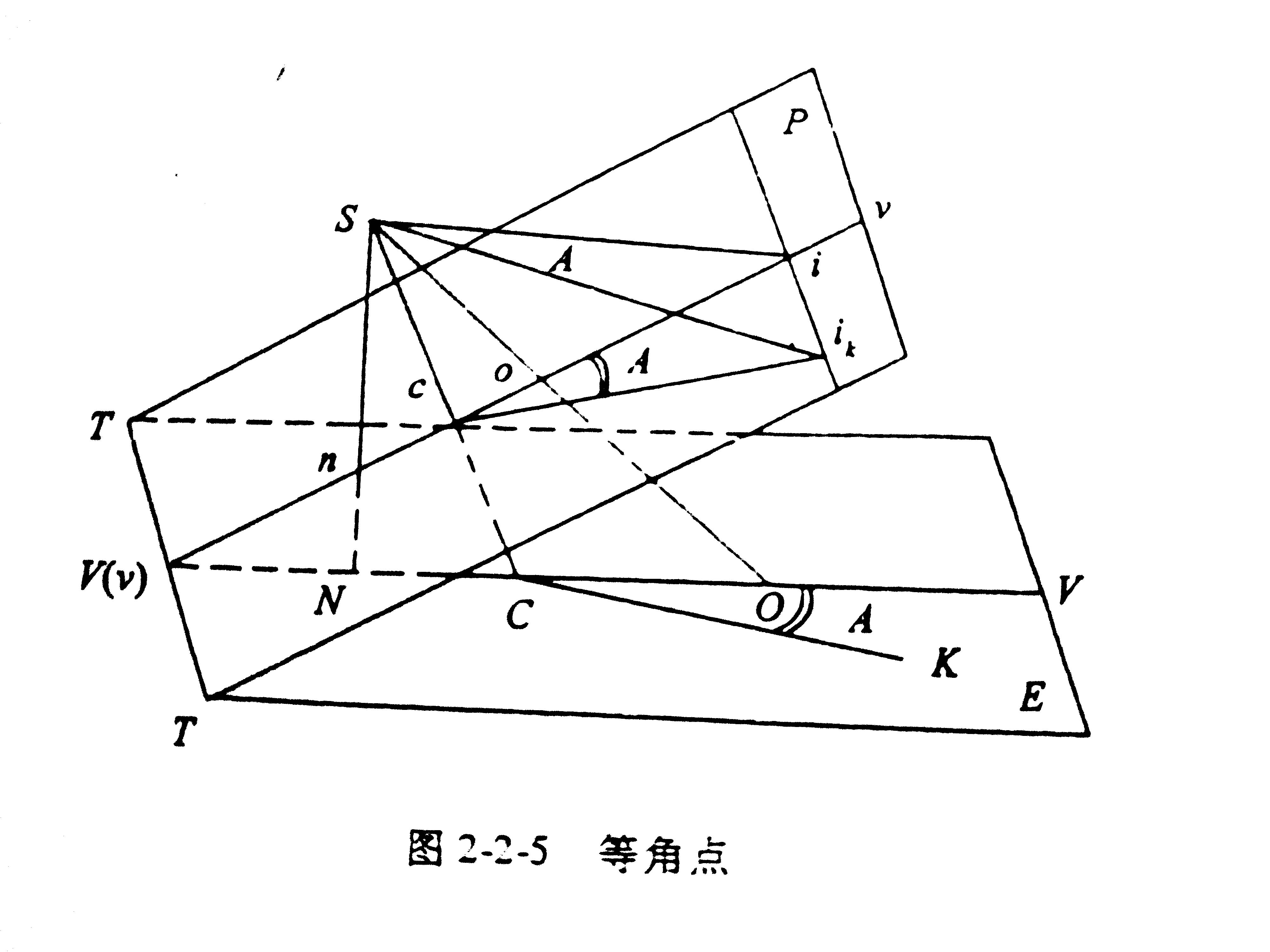
注意到△Siik与△ciik均为Rt△,又∵Si=ci,∴△Siik≅△ciik,∴∠iSik=∠icik
- 等角点的性质:以等角点为顶点的对应角相等。
- 等比线的性质:过等比线的水平面P0是理想的水平相片,等比线是理想水平相片与航摄相片的交线,等比线上的相片比例尺等于水平相片的摄影比例尺f/H,不受像片倾斜的影响。
-
框标坐标系
以框标中心为原点,两对边机械框标的连线为x轴y轴的右手坐标系。x轴的方向与航向一致。
-
像平面坐标系o-xy :仿射标架(平面直角坐标系)(x,y)
像平面坐标系是以像主点为原点与框标坐标系x,y轴方向一致的坐标系
-
像空间坐标系S-xyz :空间仿射标架(x,y,−f)
(x,y,−f)即该点的齐次坐标。
与点的齐次坐标的定义有一点不同的是,射影几何中一般直接取So为单位向量,而摄影测量用So方向的单位向量。
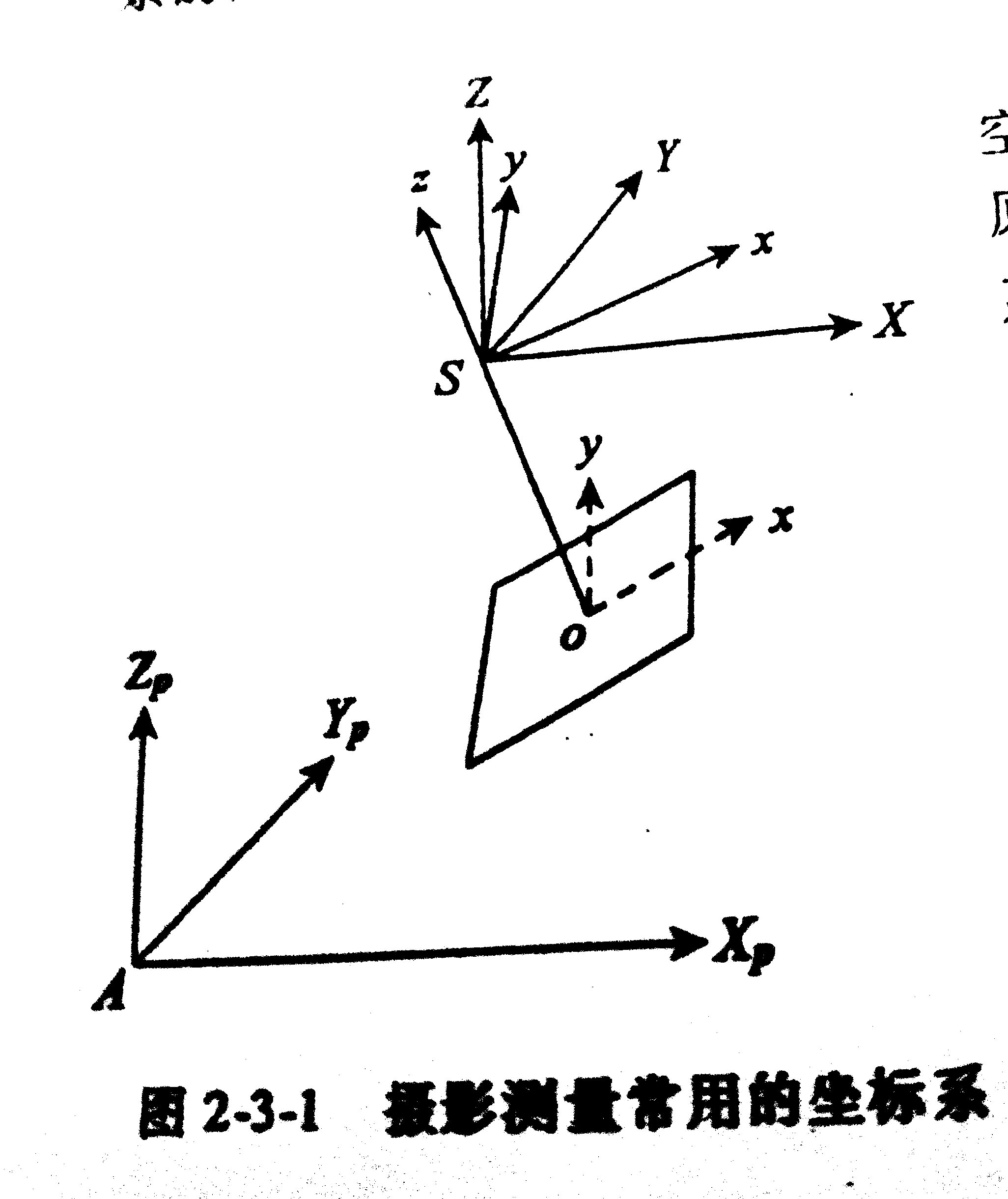
-
像空间辅助坐标系S-XYZ
一种过渡坐标系,以S为原点,以航线方向为X轴,以铅垂方向为Z轴的右手空间直角坐标系。
-
摄影测量坐标系A-XpYpZp
一种过渡坐标系,通常以地面上的某一点A为原点,坐标轴与像空间辅助坐标系一致。
-
物空间坐标系O-XtYtZt
物体所在的空间直角坐标系,在小范围内可以视为左手直角坐标系
-
内方位元素:x0,y0,f
确定摄影机的镜头中心(严格的说是镜头的像方节点)相对于影像位置的参数
三个参数:像主点在框标坐标系的坐标x0,y0以及主距f。
已知框标坐标系,内方位元素唯一确定像平面上点的齐次坐标。
内方位元素是已知的。
-
外方位元素:Xs,YS,Zs,φ,ω,κ
确定影像或摄影光束在摄影瞬间的空间位置和姿态的参数
六个参数:S在物空间坐标系的坐标(Xs,YS,Zs)和三个转角。
三个角的旋转顺序是yxz。
参见坐标系的旋转与欧拉角
定义一个从像空间辅助坐标系到像空间坐标系的坐标旋转变换
旧坐标为P=(X,Y,Z),新坐标为p=(x,y,−f)
按yxz的顺序有:
P=Rp=Ry(φ)Rx(ω)Rz(κ)p
旋转阵R即:
R=Ry(φ)Rx(ω)Rz(κ)
其中
Rx(θ)=⎝⎛1000cosθsinθ0−sinθcosθ⎠⎞
Ry(θ)=⎝⎛cosθ0sinθ010−sinθ0cosθ⎠⎞
Rz(θ)=⎝⎛cosθsinθ0−sinθcosθ0001⎠⎞
因为多个正交阵的乘积依然为正交阵,故R−1=RT,故p=RTP
在物空间坐标系中,S(Xs,Ys,Zs),A(XA,YA,ZA),a为A在以S为射心的中心投影下的像,a的像空间坐标和像空间辅助坐标分别为(x,y,−f)和
(X,Y,Z)
由SA⃗=λSa⃗知:
X=Y=Z=λ1(XA−XS)λ1(YA−YS)λ1(ZA−ZS)
又(x,y,−f)T=RT(X,Y,Z)T
所以
(共线条件方程式、共线方程)
⎝⎛xy−f⎠⎞=λRT⎝⎛XA−XSYA−YSZA−ZS⎠⎞
(已知物方坐标,求像方坐标)
它的逆变换为
⎝⎛XAYAZA⎠⎞=λR⎝⎛xy−f⎠⎞+⎝⎛XSYSZS⎠⎞
(已知像方坐标,求物方坐标)
航摄像片是地面景物的中心投影,地图则是地面景物的正(射)投影。
像点位移:由于地形起伏和像片倾斜而引起的像的位置的移动。
由前述结论:由等角点引出的对应角相等可知,从等角点出发,任意像点的方向角与水平像片上相应方向线的方向角相等。
方向角的定义:以c为极点,以等比线负向为极轴的极角。(根据课本自己的定义)
设A点在P,P0上的对应点为a,a0,像点位移δα=∣ca⃗∣−∣ca0⃗∣,像点位移与像片倾角α,像距ca以及方向角ψ有关,在等比线上无位移。在主纵线上位移最大。
(公式未经证明)
δα=−frc2sinψsinα
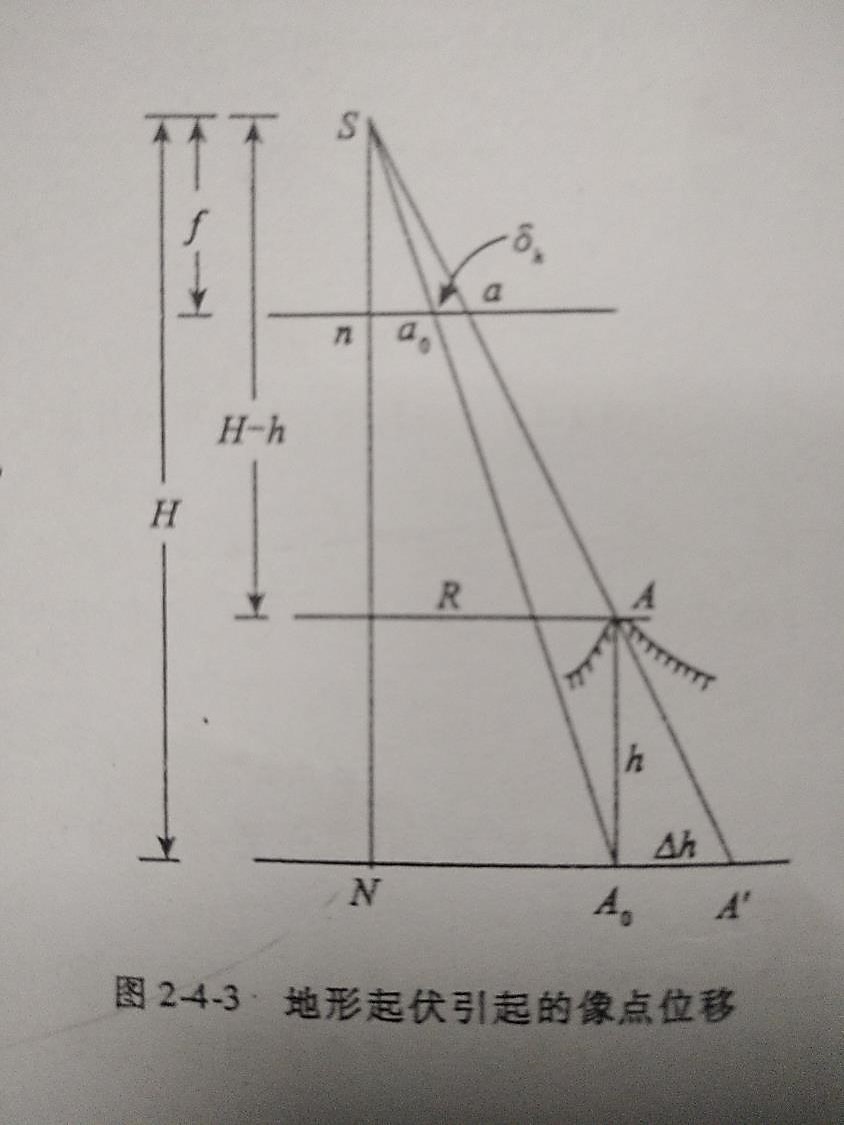
设像片水平,地面点A距基准面的高差为h,A在基准面的正投影为A0,A和A0的像为a、a0。
因地形起伏引起的像位移记为δh,也称为像片上的投影差。A在基准面上的中心投影为A'。称A0A′为地面上的投影差,记为Δh,将a到像底点的距离为r。H为航高
由相似关系:
hΔh=fr
δh=HfΔh=Hrh
Δh=H−hRh
构像比例尺:在航摄像片上某一线段影像的长度与地面上相应线段长度之比。
只有当像片与地平面平行时,像片上任意线段的比例尺都相等。




